Recently, I was gifted a Traser H3 watch from my wonderful wife. While this watch is beautiful, it has a fantastically unique feature. It uses nuclear fission (through radioactive decay) to light the hands of the watch so that it is possible to read the time when it is dark out. Don’t be scared: READ THE FACTS!
Figure 1: Watch in the day and in the night
Is Tritium Safe?
I see a question like this on just about every watch forum that uses tritium. Yes it is safe, here is why:
Everyone on earth is subject to a significant amount of natural radiation; this can come from the earth’s atmosphere, the ground, and even the foods you eat. Radioactive isotopes can be found in many different foods. A couple of the largest sources of radiation you encounter on a daily basis are mineral water, mushrooms, and (especially) bananas. A calculated example shows that consuming 1 banana every other day causes the same dose as breaking a watch equipped with tritium (1GBq of activity) and absorbing 100% of it. If you calculate it out [1] absorbing 100% of the radiation in this type of watch is equivalent to the amount of radiation your body naturally absorbs over the course of 1.3 days on earth. Also, it is important to note that the type of radiation tritium emits is so weak it can only penetrate about 6mm of air before it runs out of energy [http://en.wikipedia.org/wiki/Tritium], in other words, you will never be able to absorb 100% of a sample even if you tried.
Figure 2: A tritium watch will cause you no harm
Background information on Tritium
This watch produces light by using tritium (T or 3H) sealed in a glass tube coated in a phosphorus material. The watch lights up by using the tritium as an electron emitter through beta radiation. Each electron is emitted with a maximum energy of 18.6 keV and an average energy of 5.7 keV [2]. If this system were 100% efficient then about 1.82e12 photons would be emitted per second at 532 nm. However, I am sure that this method is not 100% efficient, I guessed 80% but I am unable to find any sources for this.
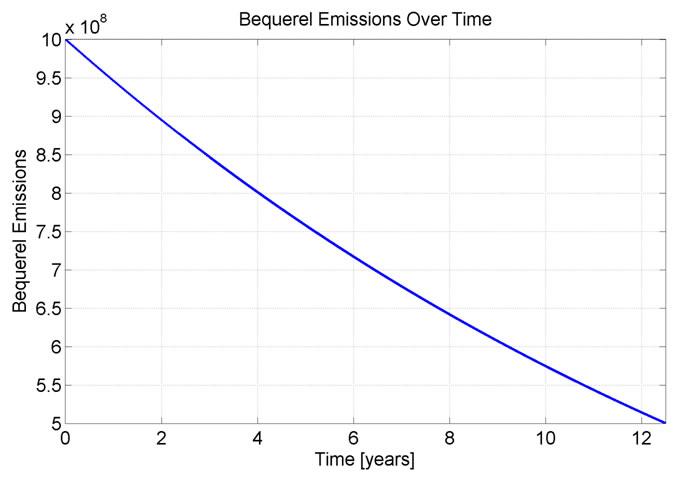
The watch has been measured to emit a maximum of 1Giga Becquerel (1 billion electrons emitted per second) [3]. With this information it is relatively straight forward to figure out how much tritium the watch holds, how bright the watch is now, and how bright it will be in the years to come. Tritium has a half life of 12.5 years, this means that in 12.5 years the watch will only emit 0.5Giga Becquerel.
Figure 3: 3H turns in to 3He or Helium plus a little bit of energy
The Process
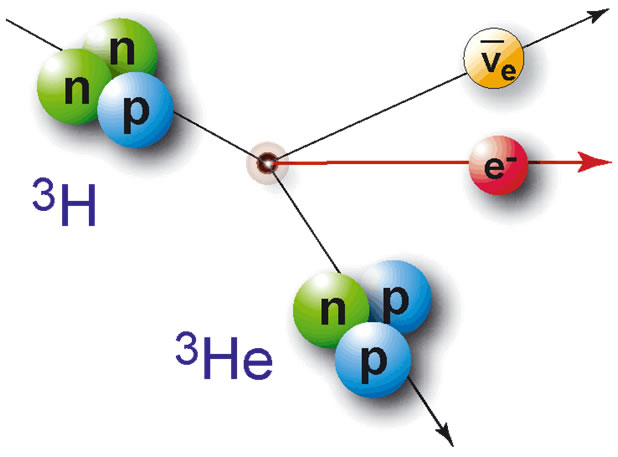
First the tritium decays and turns from 3H to 3He+e-. The beta radiation in the form of an electron fly’s through the inside of the glass tube and hits a phosphor coating. The phosphor coating absorbs some of the electrons energy and releases a photon. This cycle continues till the electron runs out of energy or is stopped by the glass tube. The phosphor coating is extremely “thick” in comparison to the electron; therefore, the electron encounters thousands of these interactions before running into the glass.
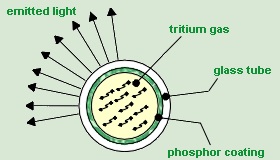
Figure 4: H -> He + e- + energy, the e- with said energy strikes the phosphor coating and generates several photons.
The Calculations
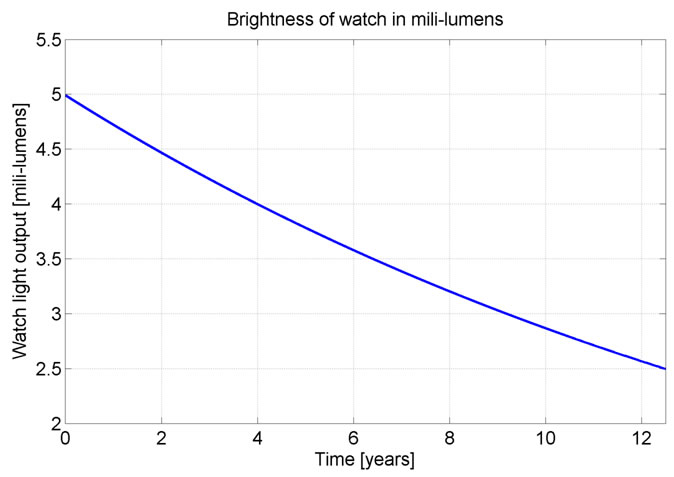
Depending on how I calculate this I get slightly different results. If I use eV and source [4] I find that on average the light that the watch emits over 12.5 years is 4.4 mili-lumens. However, if I convert eV into Joules and calculate lumens from that (683 lm/watt at 555nm green light [5]), I find that the average output of the watch is 3.6 mili-lumens, this method was used in source [6] .
While this is not a large difference I cannot figure out the difference between the two calculations (matlab code). The total emissions over time can be seen in Figure 5.
Figure 5: Tritium watch Bequerel Emissions over half life of tritium
I decided to use the eV to Joules method found in source 6 as the method for the rest of the study.
From all of this information it is possible to calculate the amount of power this watch uses to emit light (Joules/seconds or watts). I calculated this watch to use 6.58 micro-watts on average over the course of 12.5 years! This sounds like an extremely low number, but remember that it uses this many watts continuously. Or if you would like to look at it differently, this is equivalent to extracting 2.59 kilowatts from this small SMALL sample of tritium (10micro-liters) for one second. Remember the energy given off by one tritium atom is several thousand times less than what is given off by other unstable atoms like uranium.
From this it is possible to calculate the average amount of light this watch produces. When the watch is first made it produces of 5mili-lumens, over the course of 12.5 years the watch produces an average of 3.6 mili-lumens, and at 12.5 years after it was manufactured it produce about 2.5 mili-lumens of light. This was all done with the assumption that the sample is 80% efficient at converting the emitted electron into light.
Figure 6: Tritium watch light Emissions over half life of tritium
What about LED’s they’re pretty cool and efficient
This is what I really wanted to know, and why I went about doing these calculations. If someone wanted to make a watch that did this same thing with an LED and a PWM controller how long would it last on a single battery, and how many batteries would I need over a 12.5 year period?
Most LED technologies are less than 16% efficient, but for the sake of argument I decided run my calculations at 16% efficient (This is probably not realistic should be more like 10% [7]). If we assume that the driving electronics don’t draw any power then you would need 18 batteries to produce the same amount of light as this minute sample of tritium. A single battery would last less than 9 months.
I realize this is a little bit ridiculous, who needs the light on their watch on all the time? I know I do not. However, I do look at my watch once at 1am, again maybe at 3am, and then at 6am. Under this assumption, if you could integrate an LED in to the watch in this way it would work great for far longer than 12.5 years and could even be much brighter if needed.
However, most watches like mine use a substance like “Superluminova”. This type of material would not work for me. Rechargeable phosphors like “Superluminova” work quite well at first but do not work for an extended period of time. They are more meant for walking from a daylight lit room into a dark room, but they only last about 30 minutes. So if I go to bed at 11:00 pm at 1:00 am I will not be able to read my watch and I definitely will not be able to see it at 3:00 am or 6:00 am.
Figure 7: Superluminova on left and tritium on right, Charged 0 minutes prior
Figure 8: Superluminova on left and tritium on right, Charged 30 minutes prior
So what will the tritium look like in 12.5 years
I was not able to figure out a way to use math or physics to directly understand how bright this watch will really look after 12.5 years, and I was not able to find anything on the internet saying anything other than “half as bright”. Due to the fact that the eye is on a logarithmic scale and “half as bright” is on a linear scale I was required to develop my own way to “measure” what this will look like in 12.5 years. Lumens are also on a linear scale meaning that 1 lumen has half as many photons per second as 2 lumens.
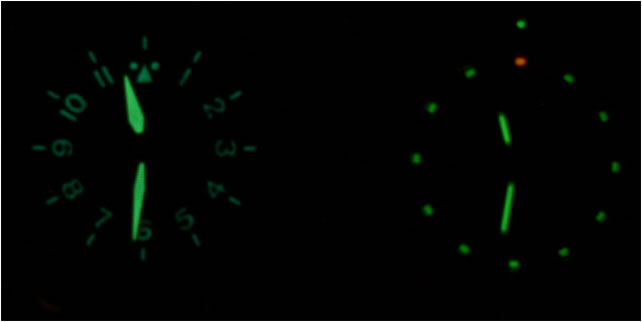
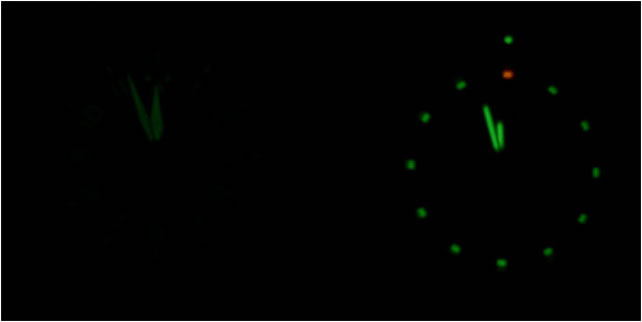
CCD cameras work on a linear scale too, and therefore can be directly related to lumens and “half as bright”. To do this experiment I took two pictures of my watch, one with a 10 seconds exposure time which I thought made the picture look very close to how bright I see it at night, and a second picture with a 5 second exposure (half the shutter speed).
This effectively cuts the number of photos the camera sees in half, and then the picture will look to a human like my watch should look in 12.5 years. My results are shown in figure 9 below.
Figure 9: (a) photo taken with 10 second exposure. (b) photo taken with 5 second exposure.
While I don’t truly know if this is what the tritium watch will look like in 12.5 years I think it is a good assumption. Maybe I’ll come back and report on in 2025.
In Conclusion
It would take a lot of batteries to match even a small amount of nuclear power, especially if that power came from a much more potent and powerful source like Uranium or Plutonium. However, unlike those two elements tritium has much less energy and cannot cause harm to the human body and once it decays it turns into harmless helium that you could use to fill birthday party balloons, or HAWB!
I am currently running a long term experiment on this watch… I report back after I have a few kids.